機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計／解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第14回は、位置度を考える上で重要な最大実体公差の「動的公差線図」について取り上げる。
前回から「最大実体公差（MMR：Maximum Material Requirement）」について取り上げています。今回は、もう1つの重要なキーワードである「包絡（ほうらく）の条件」に関する解説から始めることにします。
JIS規格（日本工業規格）では、次のように「包絡の条件」が記されています。
包絡の条件この「包絡」という用語ですが、既に連載第11回「データムを必要とする幾何公差【その4】〜姿勢公差の輪郭度〜」で登場しています。
ここでは、輪郭線の全てに対して接する曲線のことを「包絡線」として説明しています。簡単にいえば、「包絡の条件」とは「サイズ公差と幾何公差を一緒に考える」というものです。そして、これに相対するものとして、「サイズ公差と幾何公差は互いに関連を持たない」ということを示す「独立の原則」があります。独立の原則については、以前の連載「データムはどうやって決めるの？ 3D CADで考えよう」に説明があります。
「独立の原則」と「包絡の条件」
それでは、これら2つを比較しながら、包絡の条件についての理解を深めていきましょう。
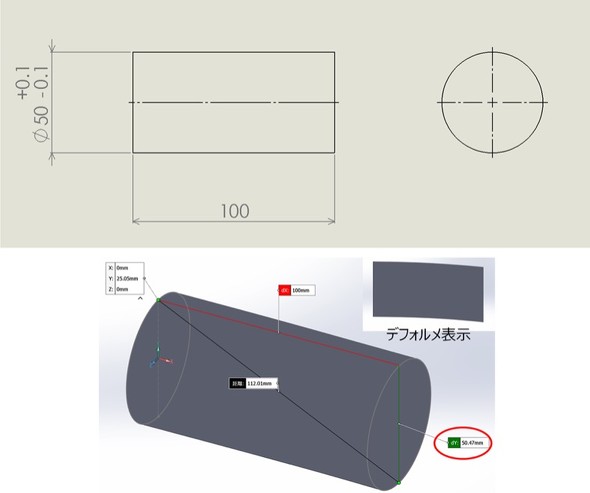
図1 独立の原則適用例 ［クリックで拡大］独立の原則では、サイズ公差は領域内50±0.1［mm］にあることが制約されますが、中心軸の「ソリ」や「うねり」は考慮されません。すなわち、例えば「真直度」や「位置度」とサイズ公差は、別々に取り扱うことになっています。
図1の場合、幾何公差が指示されていないので、この「ソリ」や「うねり」は規制されません。そのため、測定箇所によっては、サイズ公差の最大値50.1［mm］を超えることがあります。図1では、赤丸で囲んだ測定値50.47［mm］が、円柱の2点間を測定した値を示しています。
では、包絡の条件ではどうなるでしょうか？
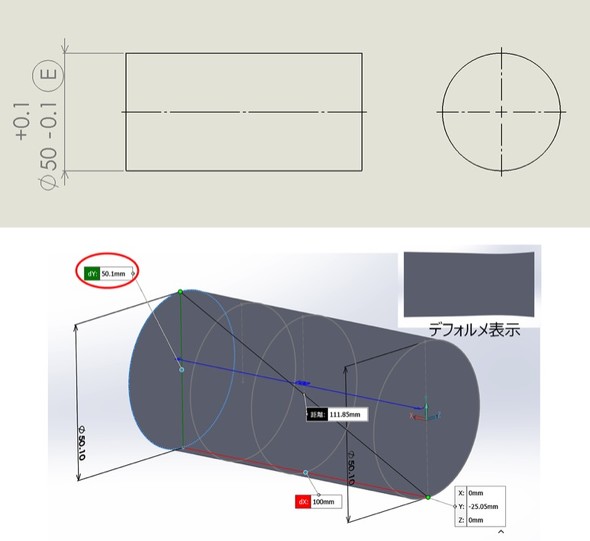
図2 包絡の条件適用例 ［クリックで拡大］図2では、「○E」と記入したことにより、「包絡の条件」が指示されています。「包絡の条件」を適用した場合、サイズ公差が50±0.1［mm］となるのは「独立の原則」の適用と同様です。
JIS規格に「包絡の条件は、単独形体、つまり円筒面または平行2平面によって決められる」とあるように、サイズ公差で示された最大実体状態（軸：最も大きい状態、穴：最も小さい状態）の範囲内に、その形体がある必要があります。そのため、サイズ公差の最大値50.1［mm］を超えることはなく、図2のように赤丸で囲んだ測定値50.1［mm］が、円柱の2点間を測定した値となります。
「独立の原則」を比較対象に、「包絡の条件」と「最大実体公差」の関係について説明しました。
Copyright © ITmedia, Inc. All Rights Reserved.
"重要な" - Google ニュース
April 02, 2020 at 08:00AM
https://ift.tt/39xXusr
位置度を考える上で重要な「最大実体公差」の「動的公差線図」 - ＠IT MONOist
"重要な" - Google ニュース
https://ift.tt/37j3R1J
Shoes Man Tutorial
Pos News Update
Meme Update
Korean Entertainment News
Japan News Update
No comments:
Post a Comment